| 17 多角形 | 月 日( ) |
| 17 多角形 | 月 日( ) |
| 1 | 江戸川学園取手高校 (R4年) ★★★ | 5 | 東海高校 (R4年) ★★★ |
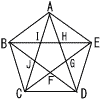 1辺の長さが2である正五角形ABCDEの5本の対角線の交点を右図のようにおき,五角形FGHIJをつくるとき, [(3)は解答手順も記述しなさい。] 1辺の長さが2である正五角形ABCDEの5本の対角線の交点を右図のようにおき,五角形FGHIJをつくるとき, [(3)は解答手順も記述しなさい。](1) ∠ABIの大きさを求めなさい。 (2) 対角線ACの長さを求めなさい。 (3) 正五角形FGHIJの面積は,正五角形ABCDEの面積の何倍か答えなさい。 |
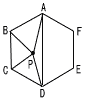 1辺の長さが6cmの正六角形ABCDEFがあり,四角形ABCDの内部に点Pをとると,△PAB,△PBCの面積がそれぞれ10√3cm2,8√3cm2であるとき, 1辺の長さが6cmの正六角形ABCDEFがあり,四角形ABCDの内部に点Pをとると,△PAB,△PBCの面積がそれぞれ10√3cm2,8√3cm2であるとき,(1) △PDAの面積は[ ]cm2である (2) 点Pを通り,対角線ADに平行な直線と辺ABの交点をQとするとき,線分AQの長さ[ ]cmである。 (3) 辺BC上の点Rを,線分PRが辺BCに垂直となるようにとったとき,線分BRの長さ[ ]cmである。 |
||
| 2 | 市立西京高校 (R5年) ★ | 6 | 都立墨田川高校 (R4年) ★★★ |
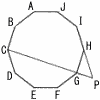 正十角形ABCDEFGHIJ において,直線CGと直線HI の交点をPとする。∠CPI の大きさを求めよ。 正十角形ABCDEFGHIJ において,直線CGと直線HI の交点をPとする。∠CPI の大きさを求めよ。 |
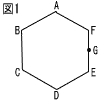 六角形ABCDEFは1辺が3cmの正六角形で,点Gは辺EFの中点である。 六角形ABCDEFは1辺が3cmの正六角形で,点Gは辺EFの中点である。(1) 図1において,頂点Bと点Gを結んでできる線分BGの長さは何cmか。 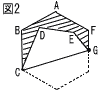 (2) 図2は,図1において,頂点Cと点Gを結んでできる線分CGを折り目にして,四角角形CDEGを五角形ABCGFに重なるように折った場合を表している。斜線で示された図形の面積は何cm2か。 (2) 図2は,図1において,頂点Cと点Gを結んでできる線分CGを折り目にして,四角角形CDEGを五角形ABCGFに重なるように折った場合を表している。斜線で示された図形の面積は何cm2か。 |
||
| 3 | 國學院久我山高校 (R5年) ★★ | ||
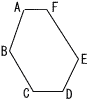 図のような,6つの内角の大きさがすべて等しく,周の長さが39の六角形ABCDEFがある。AB=8,BC=7,CD=6のとき,EF=( )となる。 図のような,6つの内角の大きさがすべて等しく,周の長さが39の六角形ABCDEFがある。AB=8,BC=7,CD=6のとき,EF=( )となる。 |
|||
| 4 | 桐蔭学園高校 (R6年) ★ | 7 | 駿台甲府高校 (R6年) ★ |
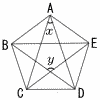 図のように,正五角形ABCDEがある。このとき,∠xの大きさは[ ]°,∠yの大きさは[ ]°である。 図のように,正五角形ABCDEがある。このとき,∠xの大きさは[ ]°,∠yの大きさは[ ]°である。 |
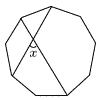 右の図の正九角形において,∠xの大きさを求めよ。 右の図の正九角形において,∠xの大きさを求めよ。 |
||