 図形 |
２２ 直方体 | 月 日（ ） |
| 図形 |
２２ 直方体 | 月 日（ ） |
| １ | 岩手県立高校 （Ｒ５年） ★★★ | ４ | 早大本庄高校 （Ｒ４年） ★★★ |
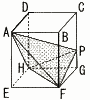 右の図は,AB＝6cm,AD＝5cm,AE＝7cmの直方体ABCD-EFGHです。(1) 線分AFの長さを求めなさい。 (2) 辺CG上にPG＝2cmとなるような点Pをとったとき,四面体AHFPの体積を求めなさい。 |
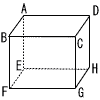 図は,AB=3,AD=6,AE=6の直方体ABCD-EFGHである。辺 BF,辺DH上にそれぞれ点 I,Jを4点A,I,G,Jが同じ平面上にあるようにとる。Bl=3のとき四角形AIGJの面積 Sを求めよ。 |
||
| ２ | 洛南高校 （Ｒ４年） ★★★ | ５ | 中央大杉並高校 （Ｒ４年） ★★★ |
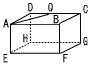 AB＝4,AD＝AE＝2√3である直方体ABCD-EFGHがあります。また,辺DC上に点Qがあり,AQ=4です。(1) DQの長さを求めなさい。 (2) 点Pは,AP＝4を満たしながら面ABCD上をBからQまで移動します。Pが描く曲線の長さを求めなさい。 (3) 点Pは,AP=4を満たしながら直方体の表面上を一周します。 (ｱ) Pが描く曲線の長さ (ｲ) 線分APが通過してできる面の面積の和 |
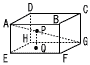 AB＝6,AD＝AE＝3の直方体ABCD-EFGHがあります。対角線AG上にAP:PG＝1:2となるように点Pをとり,Pから面EFGHに垂線をひき,その交点をQとします。(1) PQの長さを求めなさい。 (2) EPの長さを求めなさい。 (3) 三角すいP-AEHの体積を求めなさい。 (4) 点Aから3点E,H,Pを通る平面におろした垂線の長さを求めなさい。 |
||
| ３ | 福岡県立高校 （Ｒ６年） ★★ | ６ | 西大和学園高校 （Ｒ６年） ★★★ |
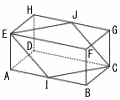 図は,AB＝8cm,BC＝4cm,AE＝4cmの直方体ABCDEFGHを表している。(1) 辺EF上に点P,辺FG上に点Qを,AP＋PQ＋QCの長さが最も短くなるようにとる。 このとき,線分PQの長さを求めよ。 (2) 辺ABの中点を I, 辺HGの中点をJとし,四角形EICJをつくったものである。 辺EF上に点Kを,EK＝KCとなるようにとるとき,四角すいKEICJの体積を求めよ。 |
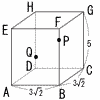 図のように,底面が一辺の長さ3√2の正方形で,高さが5の直方体がある。点P,Qはそれぞれ辺 BF,辺DH上の点で,FP＝1,DQ＝1である。このときPQの長さは[ア ]
である。三角形PACの面積は[イ ] であり,三角錐PACQの体積は[ウ ] である。 |
||
