| 28 展開図・投影図 | 月 日( ) |
| 28 展開図・投影図 | 月 日( ) |
| 1 | 東北学院高校 (R5年) ★ | 5 | 山形県立高校 (R5年) ★ |
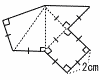 図は,ある立体図形の展開図です。この展開図を組み立ててできる立体の体積を求めなさい。 図は,ある立体図形の展開図です。この展開図を組み立ててできる立体の体積を求めなさい。 |
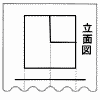 右の図は,投影図の一部である。この図から考えられる立体の見取図として適切でないものを,次のア~工から1つ選び,記号で答えなさい。 右の図は,投影図の一部である。この図から考えられる立体の見取図として適切でないものを,次のア~工から1つ選び,記号で答えなさい。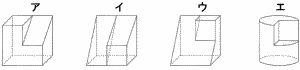 |
||
| 2 | 中央大附属高校 (R4年) ★ | 6 | 山口県立高校 (R4年) ★ |
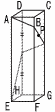 図のような,辺の長さが1である正方形を底面とし,高さが4の正四角柱ABCD−EFGH がある。点Pは頂点Aを出発して正四角柱のすべての側面
を通るように進み頂点Eまで動く。点Pが辺DHの中点を経由して最短経路で移動するとき,点Pの描く線の長さを求めなさい。 図のような,辺の長さが1である正方形を底面とし,高さが4の正四角柱ABCD−EFGH がある。点Pは頂点Aを出発して正四角柱のすべての側面
を通るように進み頂点Eまで動く。点Pが辺DHの中点を経由して最短経路で移動するとき,点Pの描く線の長さを求めなさい。 |
立体Xの体積をV,立体Yの体積をV'としたとき,体積の整数比V:V'を求めなさい。 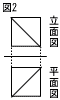 |
||
| 3 | 近大附属和歌山高校 (R4年) ★★ | 7 | 筑波大附属坂戸高校 (R4年) ★ |
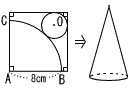 図のように,正方形の画用紙から半径が8cm,中心角が90°のおうぎ形ABCと円Oを切り取って,円すいを作ることにした。ただし,円Oは正方形の2辺に接している。画用紙の厚みやのりしろは考えないものとする。 図のように,正方形の画用紙から半径が8cm,中心角が90°のおうぎ形ABCと円Oを切り取って,円すいを作ることにした。ただし,円Oは正方形の2辺に接している。画用紙の厚みやのりしろは考えないものとする。(1) 円Oの半径を求めなさい。 (2) 画用紙の1辺の長さを求めなさい。 |
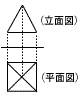 図は,ある立体の投影図です。立面図は正三角形,平面図は1辺の長さが2cmの正方形です。 図は,ある立体の投影図です。立面図は正三角形,平面図は1辺の長さが2cmの正方形です。 (1) この立体の名称を答えなさい。 (2) この立体の表面積を求めなさい。 (3) この立体の体積を求めなさい。 |
||
| 4 | 筑波大駒場附属高校 (R6年) ★★★ | (2) 立体Kにおいて,2点A,Cを結ぶ線分ACの長さを求めなさい。 (3)立体Kにおいて,4点A,B,C,Dを頂点とする三角すいA-BCDの体積を求めなさい。 |
|
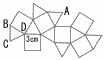 図は,ある立体Kの展開図です。立体Kのすべての面は正三角形または正方形であり,辺の長さはすべて3cmです。図のなかの4点A,B,C,Dは,それぞれ立体Kの頂点を表しています。 図は,ある立体Kの展開図です。立体Kのすべての面は正三角形または正方形であり,辺の長さはすべて3cmです。図のなかの4点A,B,C,Dは,それぞれ立体Kの頂点を表しています。この展開図を組み立ててできる立体Kについて,  (1) 立体Kの体積を求めなさい。必要があれば,立方体の見取図を用いて考えなさい。 (1) 立体Kの体積を求めなさい。必要があれば,立方体の見取図を用いて考えなさい。 |
|||