 データの活用 |
８ 場合の数１ | 月 日（ ） |
| データの活用 |
８ 場合の数１ | 月 日（ ） |
| １ | 桐光学園高校 （Ｒ４年） ★★ | ６ | 都立国分寺高校 （Ｒ４年） ★★ |
| 6個の数字0,1,2,3,4,5がある。この中から異なる4個の数字を取り出して並べてできる4桁の整数のうち,奇数は全部で何個あるか。 |
1,2.,3の数字を1つずつ書いたカード[1],[2],[3]があり,[1]のカードが2枚,[2]のカードが2枚,[3]のカードが1枚,合計5枚のカードが袋の中に入っている。 この袋の中からカードを1枚ずつ続けて3回袋に戻さずに取り出す。 1枚目のカードに書かれた数字を百の位の数,2枚目のカードに書かれた数字を十の位の数,3枚目のカードに書かれた数字をーの位の数とする3桁の整数をつくるとき,できる3桁の整数は全部で何通りあるか。 |
||
| ２ | 東海大付属浦安高校 （Ｒ６年） ★★ | ||
| もも9個,梨3個をA,B,Cの3人に4個ずつ配ります。配り方は全部で[ ]通りになります。 |
|||
| ３ | 桃山学院高校 （Ｒ６年） ★★ | ７ | 福岡大附属大濠高校 （Ｒ４年） ★★★ |
| x＋y＋z＝9を満たす自然数x,y,zの組は何通りありますか｡ただしzはx以下の数とします。 |
 右の図のように縦横等問隔に16個の点が並んでいる。これらの点の中から4個の点を選んで正方形をつくる。正方形は全部で[ ]個できる。 |
||
| ４ | ラ・サール高校 （Ｒ５年） ★★★ | ８ | 早稲田佐賀高校 （Ｒ４年） ★★★ |
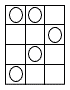 図のように,縦4マス,横3マスの長方形のマス目にいくつかの碁石を並べることを考える。縦に2つは続かない並べ方は何通りあるか。次の場合について答えよ。(1) 碁石を6個並べるとき (2) 碁石を5個並べるとき (3) 碁石を4個並べるとき |
箱の中に の5枚のカードが入っている。この箱の中から3枚を取り出し,取り出した順番に一の位,十の位,百の位として3桁の整数を作る。(1) 作られる3桁の整数は全部で何通りあるか。 (2) 作られる3桁の整数が500より大きくなる確率を求めよ。 (3) 作られる3桁のすべての整数の平均値を求めよ。 |
||
| ５ | 早大高等学院 （Ｒ６年） ★ | ９ | 早稲田実業高等部 （Ｒ６年） ★★ |
| 大小2つのさいころを投げ,大きいさいころの目を十の位の数,小さいさいころの目を一の位の数とする,2けたの数mを作る。次の条件を満たすmは,それぞれ何個あるか求めよ。 (1) 3の倍数である。 (2) 素数である。 |
 の4枚のカードを  のように並べて式を作る。例えば, と並べるとその値は112である。式の値が3の倍数となるような並べ方は全部で何通りあるか。 |
||
