 データの活用 |
１２ 数列１ | 月 日（ ） |
| データの活用 |
１２ 数列１ | 月 日（ ） |
| １ | 宇都宮短大附属高校 （Ｒ４年） ★★ | ５ | 近畿大附属和歌山高校 （Ｒ５年） ★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3で割ると2余る自然数のうち小さい方から数えて7番目の数と,5で割ると3余る自然数のうち小さい方から数えて10番目の数の和は[ ]である。 |
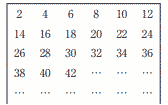 右の図のように,連続する偶数を2から順に6個ずつ並べる。(1) この図で上から6番目で左から4番目の数を求めよ。 (2) この図で上からm番目で左からn番目の数をm,nを用いて表せ。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ２ | 明治学院東村山高校 （Ｒ５年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
以下のように分数が規則的に並んでいる。39番目の分数を答えな さい。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ３ | 尚絅学園高校 （Ｒ５年） ★ | ６ | 立命館慶祥高校 （Ｒ３年） ★★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
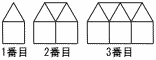 図のように,1辺が1cmの正三角形と正方形を規則的に並べて,1番目の図形,2番目の図形,3番目の図形,……と呼ぶことにします。(1) 5番目の図形について,並んでいる正三角形の個数を求めなさい。 (2) n番目の図形について,並んでいる正三角形と正方形の個数の合計をnを用いて最も簡単な式で表しなさい。 (3) 1番目の図形の周りの長さは5cmです。周りの長さが 25cmである図形には,正三角形と正方形が合わせて何個並んでいますか。 |
下の図のように,奇数が書かれた正方形をある規則にしたがって並べて図形をつくり,2番目以降の図形は,図形の左下にある正方形に色を塗る。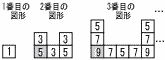 (1) 4番目の図形において,色を塗った正方形に書かれた数を求めなさい。(2) n番目の図形において,色を塗った正方形に書かれた数を,nを用いた式で表しなさい。 (3) 1番目の図形から50番目の図形において,109と書かれた正方形は全部で何個あるか,求めなさい。計算過程も解答欄に書きなさい。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ４ | 東洋大京北高校 （Ｒ６年） ★ | ７ | 芝浦工大附属高校 （Ｒ６年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
下の図のように,ある規則に従って自然数を並べます。
(1) 30は何段目の左から何番目にあるか答えなさい。 (2) x段目の一番右の数をxを使って表しなさい。 (3) x段目の左からy番目の数をx,yを使って表しなさい。 |
座標平面上に原点Oから始まる渦巻線があ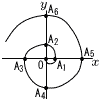る。 渦巻線と座標軸との交点は,0に近い方から次のように定める。x軸の正の方向にA1,A5,A9,…… y軸の正の方向にA2,A6,A10,…… x軸の負の方向にA3,A7,A11,…… y軸の負の方向にA4,A8,A12,…… このとき,線分OAkの長さはkとする。例えば,OA5＝5である。 (1) 次の空欄をうめなさい。なお,(1)は答えのみでよい。 (ｱ)点A2024の座標は[ ]である。 (ｲ)3点A14,A15,A16を頂点とする三角形の面積は[ ]である。 (2) kを正の整数とし,3点Ak,Ak+1,Ａk+2を頂点とする三角形の面積をSkとする。例えば,(1)(ｲ)の面積はS14である。 (ｱ) Sk+1－Ｓk＝35となるkの値を求めよ。 (ｲ) 2つの正の整数a,bに対して,Sa－Sb＝48となる(a,b)の組を求めよ。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
