データの活用	１６　さいころ (確率) ２	月　　　日（　　）
以下の問題では,さいころはどの目が出ることも同様に確からしいものとします。

１	群馬県立高校　（Ｒ６年）　★	５	都立立川高校　（Ｒ６年）　★
大きさの異なる2つのさいころを同時に投げて,大きいさいころの目が3以下のときは2つのさいころの目の和をXとし,大きいさいころの目が4以上のときは2つのさいころの目の積をXとする。このとき,Xが5の倍数となる確率を求めなさい。		1から6までの目が出る大小1つずつのさいころを同時に1回投げる。 　大きいさいころの出た目の数を十の位の数,小さいさいころの出た目の数を一の位の数とする2桁の整数をつくる。つくった整截を4で割った余りか3である確率を求めよ。
２	東大寺学園高校　（Ｒ４年）　★★	６	慶應義塾高校　（Ｒ４年）　★★★
大小2個のサイコロを投げて出た目の数をそれぞれA,Bとするとき,A＋Bと6の最大公約数が１となる確率を求めよ。		1つのさいころを3回投げて,１回目,2回目,3回目に出た目の数をそれぞれa,b,cとするとき, 　b＋c ＝となる確率は[　　]である｡ 　2a
３	愛光高校　（Ｒ４年）　★★★	７	市川高校　（Ｒ４年）　★★★
１つのさいころを3回投げて,出た目の数を順に十の位,一の位,小数第１位として小数をつくる。その小数の小数第１位を四捨五入した整数をAとするとき, (1) A＝45となる確率を求めよ。 (2) A≧45となる確率を求めよ。		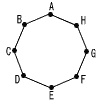右の図のように,正八角形ABCDEFGHがあり,動点Pは最初,頂点Aにいる。さいころを振って,出た目の数の分だけPは正八角形の頂点を順に反時計回りに進む。ただし,頂点Dより先の頂点に進む目が出たとき,PはDで必ず止まるものとする。例えば，さいころを2回振って出た目の数が順に6,2のとき,PはA→D→Fと動き,出た目の数が順に2,6のとき,PはA→C→Dと動く。 (1) さいころを2回振ったとき,PがAにいる確率を求めよ｡ (2) さいころを3回振ったとき,PがAにいる確率を求めよ。
４	ラ・サール高校　（Ｒ６年）　★★	８	立教新座高校　（Ｒ６年）　★★★
大,中,小の3個のサイコロを同時に投げ,出た目の数をそれぞれa,b,cとする。次のようになる確率をそれぞれ求めよ。 (1) ab＝c (2) a＋2b＝c (3) aを百の位,bを十の位,cを一の位としてできる3けたの整数が9の倍数になる。		さいころを3回続けて投げるとき,１回目,２回目,3回目に出た目の数をそれぞれa,b,cとします。このとき,2次方程式ax2＋bx＋c＝0の解について,次の確率を求めなさい。 (1) 2つの解が−2,−3となる確率 (2) −1を解にもつ確率 (3) 解が1つになる確率 (4) 解が有理数になる確率

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用