 データの活用 |
２１ 玉 (確率) １ | 月 日（ ） |
| 以下の問題では,どの玉が取り出されることも同様に確からしいものとします。 | ||
| データの活用 |
２１ 玉 (確率) １ | 月 日（ ） |
| 以下の問題では,どの玉が取り出されることも同様に確からしいものとします。 | ||
| １ | 東京都立高校 （Ｒ５年） ★ | ４ | 桜美林高校 （Ｒ５年） ★ | |||||||
| 袋の中に赤玉が1個,白玉が1個,青玉が4個,合わせて6個の玉が入っている。 この袋の中から同時に2個の玉を取り出すとき,2個とも青玉である確率は( )である。 |
袋の中に赤玉3個,青玉2個,白玉1個,合計6個の玉が入っている。この袋の中から同時に2個の玉を取り出すとき,2個の玉の色が異なる確率を求めなさい。 |
|||||||||
| ２ | 都立 西 高校 （Ｒ４年） ★★ | ５ | 都立新宿高校 （Ｒ４年） ★★ | |||||||
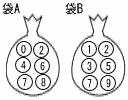 図のように,0,2,4,6,7,8の数が1つずつ書かれた6個のボールが入っている袋Aと,1,2,3,5,7,9の数が1つずつ書かれた6個のボールが入っている袋Bがある。2つの袋A,Bから同時にそれぞれ1個のボールを取り出す。 袋Aから取り出されたボールに書かれた数をa,袋Bから取り出されたボールに書かれた数をbとするとき,
|
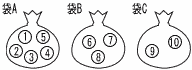 図のように,3つの袋A,B,Cがあり,袋Aの中には1,2,3,4,5の数字が1つずつ書かれた5個の玉が,袋Bの中には6,7,8の数字が1つずつ書かれた3個の玉が,袋Cの中には9,10の数字が1つずつ書かれた2個の玉が入っている。3つの袋A,B,Cから同時に玉をそれぞれ1個ずつ取り出すとき,取り出した3個の玉に書かれた数の積が6の倍数になる確率を求めよ。 |
|||||||||
| ３ | 夙川高校 （Ｒ６年） ★★★ | ６ | 立命館守山高校 （Ｒ６年） ★★ | |||||||
| 3つの袋A,B,Cのそれぞれに赤球,白球,黒球,青球が1個ずつ入っている。各袋から1個ずつ球を取り出す。 (1) 球の取り出し方は何通りあるか,求めなさい。 (2) 取り出す球の色の種類が１種類である確率を求めなさい。 (3) 取り出す球の色の種類が３種類である確率を求めなさい。 (4) 取り出す球の色の種類が２種類である確率を求めなさい。 |
2つの袋A,Bがあり,袋Aには,1,2,4,5,7の数が1つずつ書かれた5個の球,袋Bには,2,3,4,6,8,9の数が1つずつ書かれた6個の球が入っている。2つの袋から同時に1個ずつ球を取り出すとき,それぞれの球に書かれた数について,次のようにTの値を決める。
(1) Tの値が8の倍数となる確率を求めなさい。 (2) Tの値の約数の個数が3個となる確率を求めなさい。 (3) √2Tの値が整数となる確率を求めなさい。 |
|||||||||
